La grille mystérieuse...
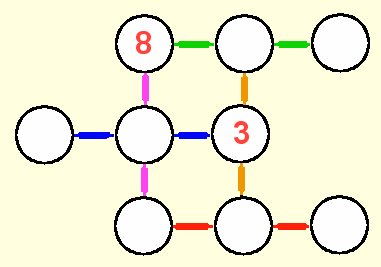
Placez dans les
cercles vides les nombres 2, 5, 6, 9, 10, 11 et 15.
La somme
des nombres contenus dans trois cercles reliés en ligne doit être
23...
Horizontalement et
verticalement, bien sûr !
Il faut trouver au moins 2
solutions différentes...
Si
tu n'y arrives pas, il y a une aide
ici...Aide n°1
Ligne ou colonne du 8 (vert ou rose)
| Ligne ou colonne du 3 (bleu ou orange)
|
Plus
d'aide ?
Aide n°2
On peut procéder
par "essais-erreur", jusqu'à que ça
marche. Mais pas au
hasard...
Par
exemple, commencer par les nombres de chaque côté
du 3.
(ligne verticale orange)
Parmi les paires de nombres choisis dans la liste :
2, 5, 6, 9, 10, 11 et 15
quelles solutions peuvent le permettre ?
Normalement, on ne devrait trouver que 4 solutions !
(Ceux qu'on évitera de placer à une intersection)
| Possible
ou impossible ? | Ils font 15 (sur la ligne du 8) car 15 + 8 = 23 | Ils font 20 (sur la ligne du 3) car 20 + 3 = 23 |
| 2 et... | 13 | 18 |
| 5 et... | 10 | 15 |
| 6 et... | 9 | 14 |
| 9 et... | 6 | 11 |
| 10 et... | 5 | 10 (on ne peut pas le prendre 2 fois !) |
| 11 et... | 4 | 9 |
| 15 et... | 0 | 5 |
Ce tableau permet aussi de trouver les nombres qui peuvent servir 2 fois
et ceux qui ne serviront qu'une fois...
Par exemple, on voit que le 2 est bien seul...
Plus
d'aide ?
Aide n°4
Pour remplir la ligne
verticale orange vous
avez dû réfléchir
autour des
compléments à 20 parmi les nombres 2, 5, 6, 9, 10, 11
et 15...
L'avantage
de commencer par les nombres de chaque côté du 3
c'est
que ça aide beaucoup pour remplir la ligne horizontale
bleue...
Car
la ligne horizontale bleue et la ligne verticale orange
ont en
commun le 3, ce qui les rend "permutables".
Ça fait
donc 2 solutions à essayer...
Une fois que quelques cases ont
été remplies, elles guident
les
recherches : en effet, comme les lignes n'ont que 3 cases,
2
cases remplies ne laissent aucune liberté pour la
3ème.